최은진의 노베부터 시작하는 확통 20 – 01강 확률적 사고

문제: 54의 양의 약수의 개수를 구하시오.
54의 소인수분해

부품을 사용하는 것을 생각. 2를 0번 () 혹은 1번 ()를 사용 가능. 그럴 때마다 이 사용 가능.
즉, 2가 2번, 3이 4번이므로

왜 이문제가 중요하냐? 이 문제는 로 공식화 되어있음. 즉, 소인수분해의 지수승의 곱으로 약수의 갯수를 구할 수 있다.

p,q,r 이 서로 다른 소수이고, l,m,n이 음이 아닌 정수일 때, 의 약수의 개수는 (l+1)(m+1)(n+1)개

A,B가 이웃하는 경우를 세서 겹치지 않게 한다.

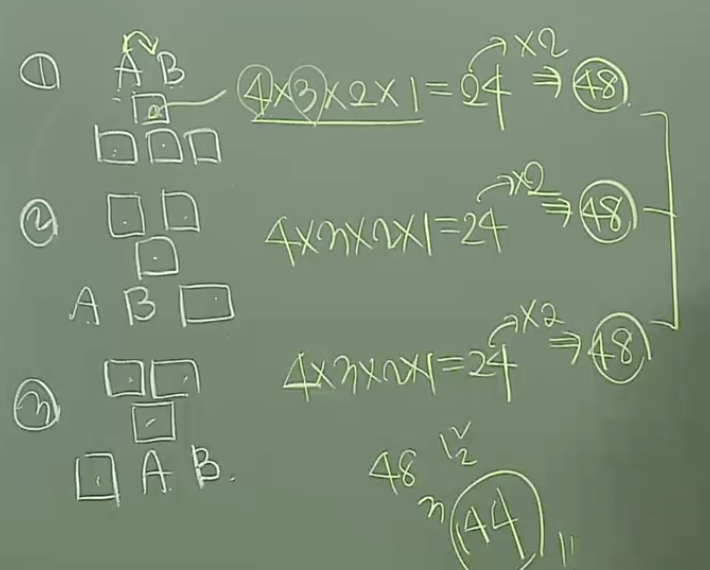
Special Lecture: 특별한 경우 수 세기
– 유형1: 색칠하기
– 유형2: 계수가 다른 부정방정식과 부등식

인접한 영역의 개수를 제외하고 가능한 경우를 세어본다.

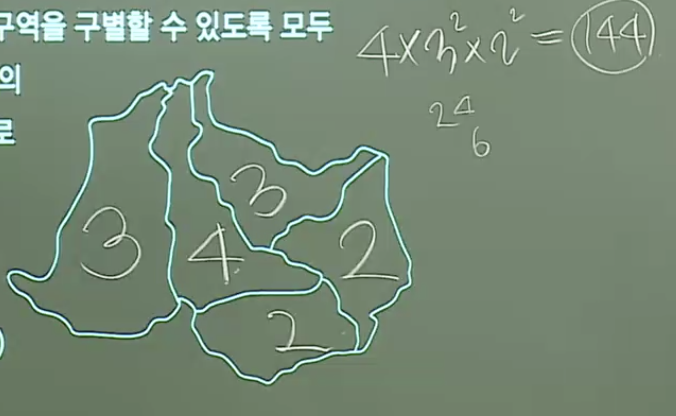
인접한 영역은 서로 다른 색을 칠해야 하므로, A=B와 A!=B의 경우가 있으므로, 해당 값에 대한 경우를 나눠야 한다. 즉,

색칠 문제는 맞닿은 면적이 많은 영역을 먼저 색칠할 것! 크게 두 가지 유형!

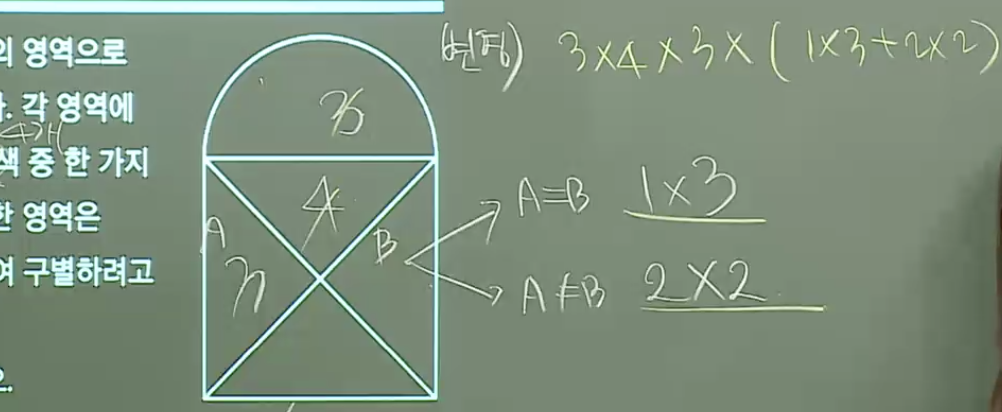
변형문제. 4가지 색일때의 경우, 역시나 인접한 영역을 A,B로 나누고 이에 들어갈 수 있는 것을 경우의 수로 계산하여 이에 대한 합을 도출.

문제: 를 만족하는 자연수 에 대하여 순서쌍 의 개수를 구하시오.
수작업 외에 방법이 없음!
(x,y,z) = (2, ?, ?) -> 2y+z=3을 만족하는 것
=> (2, 1, 1)
(1, ?, ?) -> 2y+z=6,
=> (1, 2, 2)
(1, 1, 4) => 총 3개.

문제: 을 만족하는 자연수 의 순서쌍 의 개수를 구하시오.
=> 수작업!
(x,y) = (3,1)
= (2,2)
= (2,3)
= (1,4)
= (1,5)
즉, 5개.

문제: 다음 조건을 모두 만족하는 5가지 자연수의 개수를 구하시오.
(가) 각 자리의 숫자는 1 또는 2이다.
(나) 같은 숫자가 연속해서 3번 이상 나올 수 없다.
=> 역시 각각 세어볼것. 사전식 배열!

1 1 2 1 1
1 1 2 1 2
1 1 2 2 1
1 2 1 1 2
1 2 1 2 2
1 2 2 1 1
1 2 2 1 2
=> 총 8개에, 가장 앞자리가 2일때가 있으므로 8×2 = 16 (굳이 다 셀 필요는 없음.)

문제: 집합 은 다음과 같다. 집합 에서 한 개의 원소를 선택하여 백의 자리의 수, 집합 에서 한 개의 원소를 선택하여 십의 자리의 수, 집합 에서 한 개의 원소를 선택하여 일의 자리의 수로 하는 세 자리의 수를 만들 때, 각 자리의 수가 모두 다른 세 자리의 수를 구하시오.

이 문제의 경우 의 모든 원소가 와 에, 의 모든 원소가 에 속해 있으므로 앞의 집합에서 선택한 원소 만큼을 뒤 집합에서 빼주면 된다. 즉, 경우의 수는

(응용) (완전히 겹치지 않는 경우)

{A}, {B}, {C}의 세 자리로 생각을 한다.
A= 1의 경우, B는 2가지, C는 4가지, 즉 8가지
A=2의 경우, B는 3가지, C는 4가지, 즉 12가지
=> 8+12 = 20가지

A가 먼저 나올 경우
A -> C -> B -> D
A -> B -> C -> D
D -> C => 총 3가지
이만큼 B가 먼저 나올 경우도 있으므로, 3×2 = 6가지.

01) 만의자리 = 일의자리가 같은 경우는 세가지.
1 ? ? ? 1
2 ? ? ? 2
3 ? ? ? 3
여기서 1의 경우,
1 2 1 2 1
1 2 1 3 1
1 2 3 2 1
1 3 1 2 1
1 3 1 3 1
1 3 2 3 1
총 6가지씩 3개의 경우이므로, 6×3 = 18가지

02) 모양이 각각 3개, 빨강/초록 색상. A,B는 각각 다른 셔츠와 바지. 각각 인형은 다른 색상의 셔츠와 바지.
색깔정하는 경우는 A : 2×1 2가지 B : 2×1 2가지 둘은 A의 각각의 경우에 B 가 대응되니까 곱의법칙에 의하여 4이고, 셔츠바지 정하는 경우는 셔츠를 ABC 바지를 abc라 놓으면, A 가 셔츠를 입는경우는 셔츠가 각각의 경우에 반복하여 속하는경우의수가 2이므로 3×2이고 바지도 마찬가지로 각각의 경우에 반복하여 속하는 경우의 수가 3×2 이고 둘은 동시에 일어나므로 6×6=36