최은진의 노베부터 시작하는 확통 20 – 06강 중복조합

중복조합

서로다른 n개에서 중복을 허락하고 r개를 뽑는 경우의 수:

5는 두가지 ‘종류’ 중 한 개의 구분, 그중에 뽑는 4가지. =

=> 서로 다른 2개에서 중복을 허락하여 4개를 택하는 중복조합의 수 = 4개의 과일과 (2-1)개의 막대를 일렬로 나열하는 경우의 수 = (4+2-1)개의 자리에서 4개의 과일을 놓을 자리 4개를 선택하는 조합의 수

문제: 1,2,3,4의 번호가 적힌 카드 4장의 카드 중에서 중복을 허락하여 2장의 카드를 택하는 경우의 수를 구하시오

문제: 자연수 r에 대하여 일때 의 값을 구하시오
126

중복조합 대표유형
(1)선택
ex) 서로다른 4개 피자중 중복 허락해서 5개를 선택

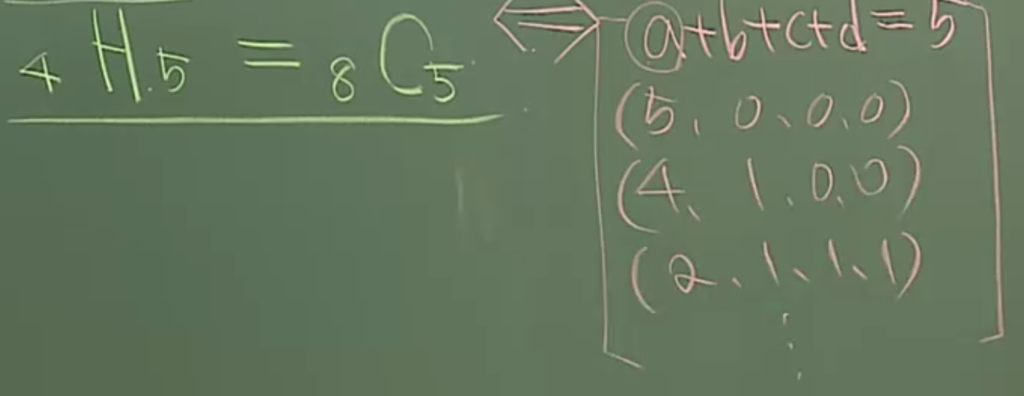
(2) 분배
ex) 같은 종류 음료 7개 중 서로다른 세 사람에게 나눠주는 방법

문제: 축구공, 농구공, 배구공 중에서 4개의 공을 선택하는 방법의 수를 구하시오. (단, 각 종류의 공은 4개 이상씩 있고, 같은 종류의 공은 서로 구별하지 않는다.)
-> 중복이 된다. 선택의 문제. 즉,

문제: 1부터 10까지 숫자가 각각 하나씩 적힌 10개의 상자가 있다. 똑같은 구슬 3개를 상자에 넣는 방법의 수를 구하시오. (단, 각 상자에 들어가는 구슬의 개수는 제한이 없다.)
-> 분배유형! a+b+…. = 3 이런 식으로 모델링 하면 좋음. 즉,

방정식의 해의 개수 구하기
– 중복조합 중 분배 유형 문제는 ‘방정식의 해의 개수를 구하는 문제’ 로 바꿔 생각하라.
– 적어도 하나씩은 받아야 한다면 미리 하나씩 주고 시작.
1) 방정식 x+y+z=r (r은 자연수)에서
(1) 음이 아닌 정수해의 개수는
(2) 양의 정수해의 개수는 $latex ^3H_{r-3} (단 r >= 3)
2) 를 전개했을 떄 서로 다른 항의 개수는

문제: 방정식 x+y+z = 17에 대하여 다음 해의 개수를 구하시오
1) 음이 아닌 정수해:
2) 양의 정수해: 하나씩 주고 함. 즉, x’+y’+z’ = 14로 계산.