최은진의 노베부터 시작하는 확통 20 - 11강~13강 조건부확률과 확률의 곱셈정리

1. 조건부확률

let says, 아래와 같은 통계자료가 있음:

	교통사고남	교통사고안남
눈이옴	3일	2일	5일
눈이안옴	5일	21일	26일
	8일	23일	31일

(1) 눈이 오고, 교통사고가 난 날이었을 확률은?
$\frac{3}{31} = \frac{n(A\cap\text{B})}{n(S)} = P(A\cap\text{B})$
(2) 눈이 오는 날이었을 떄, 교통사고까지 난 날일 확률은?
$\frac{3}{5} = \frac{n(A\cap\text{B})}{n(A)} = P(B|A)$ (조건부 확률!)

$P(B|A) = \frac{n(B\cap\text{A})}{n(A)}$
A가 일어났을 “때”, B가 일어날 확률

문제: 주사위 한 개를 던지는 시행에서 눈의 수가 6의 약수인 사건을 A, 눈의 수가 소수인 사건을 B라고 할 때, P(A|B)와 P(B|A)를 각각 구하시오.
A => {1,2,3,6} B => {2,3,5} $A\cap\text{B}$ = {2,3}
P(A|B) = $\frac{n(A\cap\text{B})}{n(B)} = \frac{2}{3}$
P(B|A) = $\frac{n(B\cap\text{A})}{n(A)} = \frac{1}{2}$

문제: 두 사건 A,B에 대하여 $P(A\cap\text{B}) = \frac{1}{9} , P(B|A) = \frac{1}{2}$ 일때 P(A)의 값을 구하시오.
2/9 가 나옴. (조건부 확률의 공식을 이용)

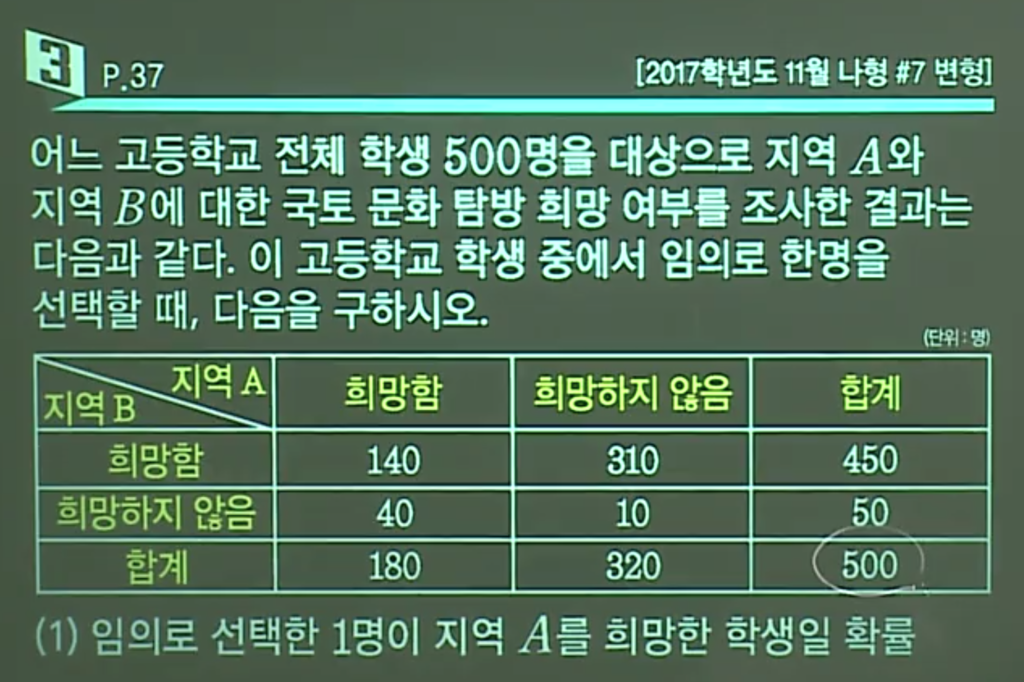
180/500 = 9/25

(2) 임의로 선택한 1명이 지역 A와 B를 모두 희망한 학생의 확률: 140/500

(3) 임의로 선택한 1명이 지역 A를 희망한 학생이었을 때, 이 학생이 지역 B도 희망한 학생일 확률: P(B|A) = $\frac{n(A\cap\text{B})}{n(A)} = \frac{140}{180}$

문제유형: 표가 주어진경우/ 주어지지 않은 경우.

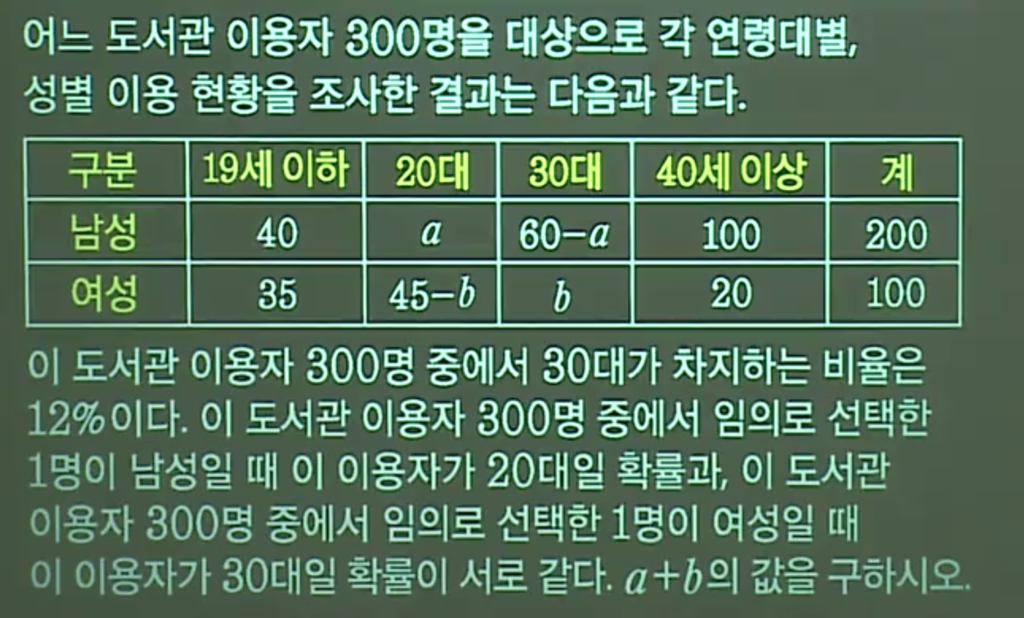
(표를 주지만 내부 값을 계산해야 하는 유형!)
30대 비율: 60-a+b = 12/100 * 300 = 36, a-b = 24

P(20대|남) = P(30대|여)

= $\frac{n(20대\cap\text{남})}{n(남)} = \frac{n(30대\cap\text{여})}{n(여)} = \frac{a}{200} = = \frac{b}{100} =$

표가 주어지지 않은 경우!

직접 그려본다.

P(여|B) = 15/40 = 3/8 * 80 = 30

확률의 곱셈정리

$P(A\cap\text{B}) = P(A) \ast P(B|A)$
ex) 주사위 두번 던져, 첫번째는 1의눈, 두번째는 3의 눈일 확률?
첫번째: 1/6 두번째: 1/6 = 1/6*1/6 = 36
ex) 5개의 공, 3개의 당첨제비가 있는 주머니에서 두번 모두 당첨제비의 확률은?
3/5 * 2/4 = 3/10
여기서는 앞의 사건이 뒤의 사건에 영향을 받음. 즉, A,B의 사건에서 P(B)가 아니라 P(B|A)로 표기해야함.

확률 달성확률

높음 0.4 0.8 = 0.32
비슷 0.5 0.6 = 0.3
낮음 0.1 0.3 = 0.03

다 합쳐주면 됨. 답은 0.65

문제: 어떤 의사가 암에 걸린 사람을 암에 걸렸다고 진달할 확률은 98%이고, 암에 걸리지 않은 사람을 암에 걸리지 않았다고 진단할 확률은 92%라고 한다. 이 의사가 실제로 암에 걸린 사람 400과 실제로 암에 걸리지 않은 사람 600명을 진찰하여 암에 걸렸는지 아닌지를 진단하였다. 이들 1000명 중 임의의 한 사람을 택했을 때, 그 사람이 암에 걸렸다고 진단받을 확률을 구하시오.

암에 걸린사람을 암이라 진단 -> 0.98
암에 안걸린 사람을 암이라 진단 -> 0.08

암에 걸린사람을 선택 -> 0.4
암에 안걸린 사람을 선택 -> 0.6

즉, 0.98*0.4 + 0.08*0.6 = 0.440 (44%)