Introduction
머신러닝이란?
컴퓨터가 배울 수 있는 능력을 프로그램을 통하지 않고 가질 수 있는 것이다. – Arthur Samuel정의
컴퓨터 프로그램이 T라는 몇몇 작업(task)들과 P라는 퍼포먼스 측정을 기본으로 하는 E라는 경험에서 배우는 것을 의미한다. 단, P로 측정된 테스크들 T가 E라는 경험을 발전(improve)시켰을 때. – Tom Mitchell정의
예: 체커(checker)
- E: 여러 게임들의 체커(아마도 게임의 룰을 의미?) 의 경험
- T: 체커를 돌리는 작업
- P: 다음 게임에서 이길 수 있는 확률
기본적으로 머신러닝은 Supervisied 와 Unsupervisied로 나눈다.
Supervised Learning: Right answer를 준다.
- Regression
- 데이터를 통한 예측으로, 2차원 그래프에서의 예측 등이 포함된다.
- Specific Numerics
- Classification
- 군집화를 통한 해당 대상의 선택을 의미한다.
- Binary (0 or 1)
Unsupervised Learning
- Find structure of bunch of data!
- Example
- 컴퓨터 클러스터 구성
- SNS관계망
- 마켓 세분화
Astronomical data analysis!
예: 칵테일 파티 문제 (cocktail party problem)
- [W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);
- svd -> single variable derivation
- 위 문법은 Octave 으로, ML 에서는 이 프로그램을 이미 많이 사용한다. 미리 예측해 보기 위해.
Model and Cost Function
Model Representation
: 예측(predict)을 위한 트레이닝 pair. 트레이닝 example. (i,j 승이 아니라 i,j는 몇번째인 것을 의미)
-
: input. input features라고도 불리며, X라고도 정의한다.
-
: output, predict (price)함수를 통해 예측하고자 하는 값으로, Y라고도 정의한다.
: 트레이닝 셋 (training set)
좀더 포멀하게 말하면, 주어진 트레이닝 셋에에서 h : X → Y 라는 함수를 통해 “learn”할 수 있게 하여 h(x)가 값 y에 대하여 “좋은” 예측자(predictor)가 되도록 만드는 것이다.
전통적으로, 함수 h는 가설(hypothesis)이라 불리며, 이미지로 표현하면 다음과 같다:
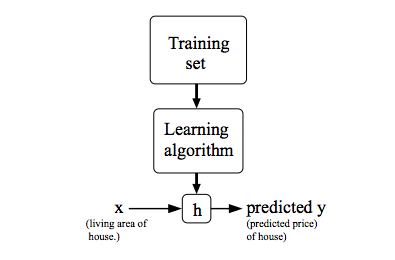
만약 우리가 예측하고자 하는 값이 “지속적(continuous)” 값이라면 (예: 주택값의 변화량) 우린 이를 regression 문제라 정의한다.
만약 y가 단순히 작은 분산값을 가질때 (예: 주어진 주거지 목록에서 주택이 집인지 아파트인지를 예측하는 문제) 우린 이를 classification 문제라고 한다.
Cost Function
hypothesis 함수의 정확도를 의미하며, 함수h의 모든 x에 대한 실제 결과 y의 모든 값들에 대한 평균적 차이를 의미한다.
위 수식을 세밀하게 말하면, 에서
는
의 제곱 혹은 예측된 값과 실제 값의 차이를 의미한다. 다르게 말해서 “제곱된 에러 함수 (squared error function)”혹은 “제곱된 중간 에러 (mean squared error)” 라고도 한다. 여기서
은 경사하강법(gradient descent)의 편의를 위해 사용되며, 제곱 함수의 미분계수(derivative)에 의해
는 상쇄된다. Cost function이 하는 일을 이미지로 정리하면:

시각적으로 생각해 볼때, 트레이닝 셋은 x-y평면에 흩어져 있다고 볼 수 있다. 여기서 우린 흩어진 데이터를 지나는 로 정의된 라인(line)을 그려볼 수 있다.
우리 목표는 최적의 라인(위에서 정의한)을 찾는 것이다. 최적의 될 가능성이 있는 라인은 이 라인에서 흩어진 트레이닝 셋간의 거리의 제곱의 평균이 최저인 것이다. 이상적인 라인은 이 라인이 모든 트레이닝 셋을 지나는 것이다. 이 경우, 은 0이 된다. 아래 이미지는 이상적인 경우인 cost function이 0이어떻게 되는지를 보여준다:
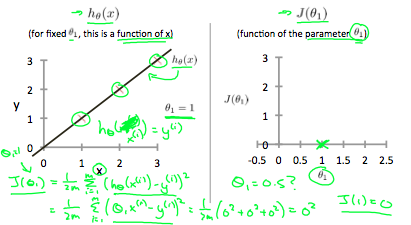
일때 우리 모델에서 모든 정점을 지나는 기울기 1을 갖는다. 이와는 대조적으로,
일때, 데이터 셋과 라인 간의 수직 거리가 상승하는 것을 볼 수 있다.
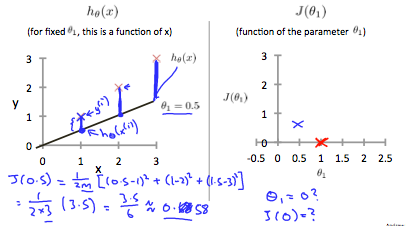
0.5일때 cost function은 0.58이며, 이런 몇몇 계산결과를 통해 아래와 같은 cost function그래프를 그릴 수 있다.
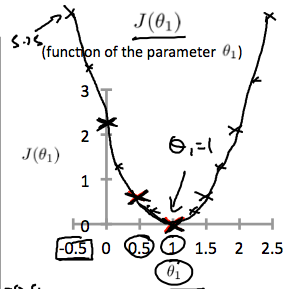
결국 우리 목표는, cost function을 최소화 시키는 것이고, 위 경우에는 이 최소 값이된다.
등고 플롯(contour plot)은 많은 등고선을 가지고 있는 그래프이다. 두개의 변수를 가지는 등고선은 같은 라인에서 상수값을 가지고 있다.
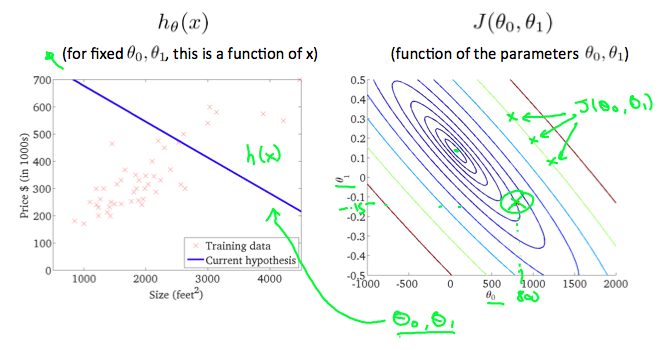
위 그래프처럼, 어떤 칼라가 가미된 “원형” 에 따라서 우린 같은 cost function값을 가진다고 예상할 수 있다. 위 그림에서 초록색 원형 그래프상의 세개의 점은 같은 결과를 가지기 때문에 같은 라인 (초록색 원형 라인)선에서 발견될 수 있다. x로 동그라미친 곳은
과
일때이다. h(x)와 등고 플랫을 통해서 아래와 같은 그래프를 그려볼 수 있다.
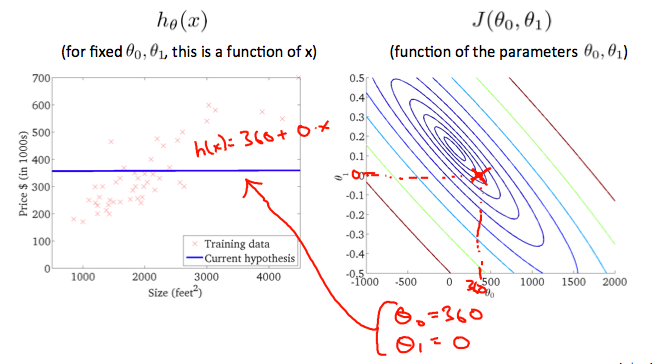
,
일때 등고 플롯에서
가 가장 중앙으로 가까워짐을 알 수 있다. 자 이제 우리 hypothesis 함수를 살짝 양수 값을 가지도록 하면 좀더 나은 결과를 가질 수 있다.
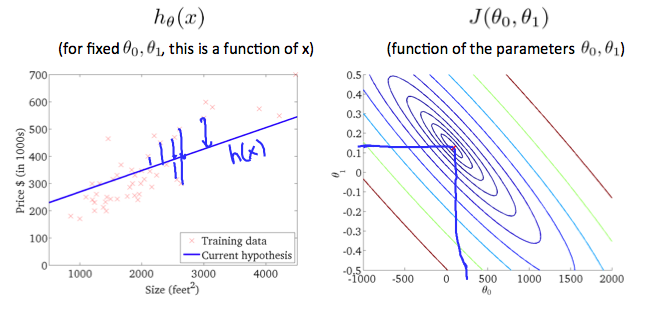
위 그래프는 ,
정도로 설정했을때의 최대한으로 최적화된 cost function이다. 오른쪽 등고 플롯의 중앙값을 우리는 최대한 서클에 근접한 내부 값의 중앙이다 라고 부를 수 있다. (이게 우리가 찾고자 하는 핵심 값.)
Gradient Descent (경사 하강법)
위에서 우린 hypothesis함수를 알았고, 데이터를 어떻게 측정해서 잘 맞게 하느냐에 대해 알았다. 이제 우린 hypothesis함수의 파라미터에 대한 측정이 필요하기 때문에, 이 부분에서 경사 하강법이 필요하게 된다.
과
에 기반한 hypothesis함수에 대한 그래프를 그린다 하면, 단순히 x,y 로는 표현하기 힘들며, hypothesis함수의 파라미터 범위와 특정 파라미터 값에서 선택된 cost 함수의 결과를 기반으로 그려볼 수 있다.
를 x축으로 두고,
을 y축으로, 그리고 cost 함수를 z축으로 둔다면, 각 정점은 특정 파라미터 값에서 cost함수의 결과가 된다
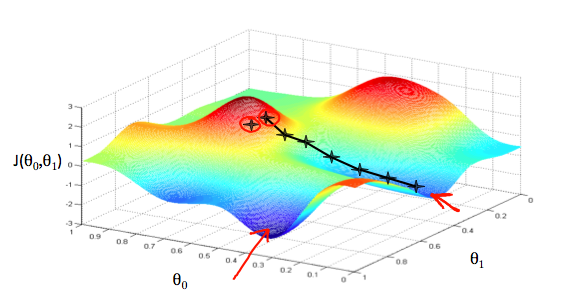
위 그래프에서 보면, 가장 낮은 지점까지 따라가는 것이 cost함수의 최적값이라는 것을 알 수 있다. 빨간 화살표가 이 그래프에서의 최소 값을 나타낸다.
이 최소값을 알기 위한 과정으로, cost함수에 대한 미분을 해서 기울기 값을 가져온다. 기울기의 접선을 알면 이것이 우리가 어디로 (위 그래프에서) 향하고 있는지를 알려주게 되는 것이다. 이를 통해 cost함수가 가장 깊은 곳으로 향하도록 만들면 된다. 각각의 단계(깊은곳으로 향하는 단계) 는 α라는 “learning rate” 파라미터로 정의한다.
예를들어 위 그림에서 별로 표시된 점이 α에 의해 각각의 단계를 나타낸다 하면, α가 작으면 단계가 많아질 것이고 α가 크다면 단계가 적을 것이다. 각각의 단계는 의 편도함수에 의해 알 수 있다. 각 단계가 어디있느냐에 따라 결과가 상이할 수 있다. 위 이미지에서 우리는 두 개의 다른 단계에 따른 두 개의 다른 최적화된 cost함수 값을 가져올 수 있다.
경사하강법 알고리즘은:
다음이 수렴할때까지 반복한다:
where j=0,1 (0,1은 index값을 의미)
각각의 j 번째 반복에서, 파라미터 은 동시다발적으로 수행되어야 한다.

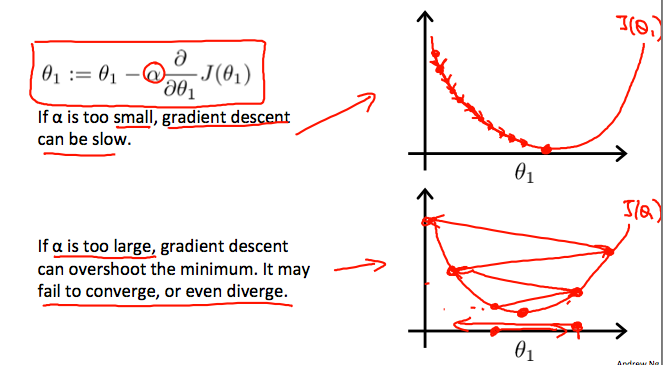
경사 하강법 알고리즘이 합리적인(reasonable) 시간내에 동작하도록 하기 위해 우린 파라미터 α를 조절할 필요가 있다. 너무 많은 α값이나 적은 값은 최소 값을 찾는데 우리 단계(step) 의 크기가 잘못됨을 의미한다. (즉, 찾는데 느리다는 의미같음)
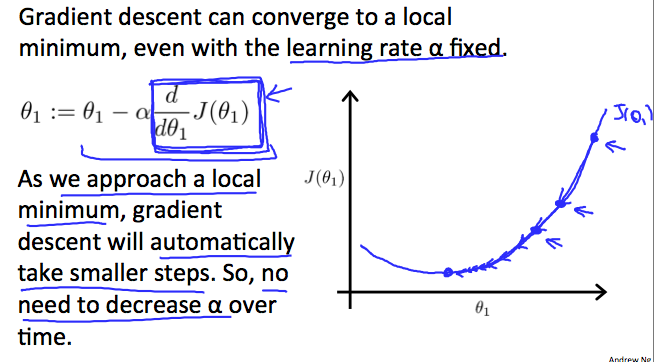
그럼 어떻게 경사하강법이 고정 단계의 크기인 α로(fixed step size α) 집중될 수 있을까?
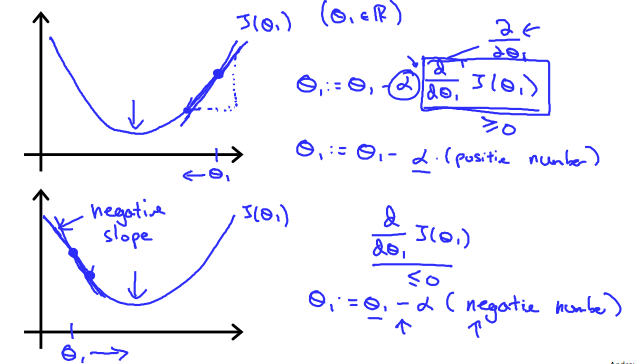
“수렴” 이라는 것에 속한 비밀은 가 0으로 향해간다는 것을 의미한다. (우리의 convex(곡선) 함수가 바닥을 향해가듯이) 최저값에서, 미분계수는 언제나 0이고 (바닥에서) 따라서 우리는 아래 수식을 얻을 수 있다:
경사하강법 for 선형 회귀(Linear Regression)
선형 회기(linear regression)를 적용하기 위해서는, 새로운 형태의 경사하강법의 식으로 유도를 해야한다. 이는 기존의 cost함수와 hypothesis함수를 치환 및 변형하여 다음과 같은 식을 유도할 수 있다.
수렴할때까지 다음을 반복:
m은 트레이닝 셋의 크기이고, 은
와 함께 동시에 변하는 상수값, 그리고
,
는 주어진 트레이닝 셋(데이터)이다. 주목할 점은, 우린 여기서
에 대해
과
로 나누었고,
에서 우린
를 곱하였다. (미분에 의해)
에 대한 미분값의 하나의 예는 아래와 같다.
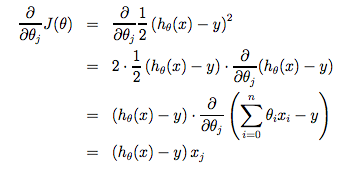
주목할 점은 만약 우리가 hypothesis함수에 대한 추측 값을 통해 경사하강법 수식을 반복한다면, hypothesis함수는 점점 정확해진다는 점이다. 이를 곧 cost함수 J위의 단순한 경사하강법이라고 부른다. 이 방법은 전체 트레이닝 셋의 모든 과정을 검사하기 때문에 이를 배치 경사하강법 (batch gradient descent)라고 한다. 주목할 것은, 경사하강법이 지역 최적값들(minima)를 가져오는 것은 자명하지만, 여기서 제시된 선형 회기를 위한 최적화 문제는 단지 글로벌(전역) 최소값에 극한된다는 것이다. 정확히 말해, J는 볼록 2차 함수(convex quadratic function)라는 것이다. 아래는 경사하강법을 2차 함수에 의거하여 최적화 한 모습을 보여준다.
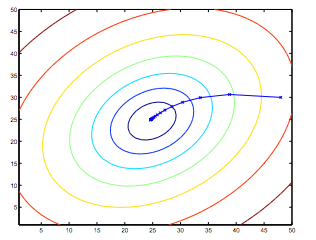
위에서 타원은 2차 함수의 등고선을 나타내고, 경사하강법에 의한 궤도는 (48,30)에서 시작 및 초기화 되었다. 그래프에서 x는 가 경사하강법에 의해 지속적으로 진행되며 최소값에 수렴한 결과를 나타낸다.