2019년 10월 24일

Coursera – Machine Learning Week2

Multiple features (variables)

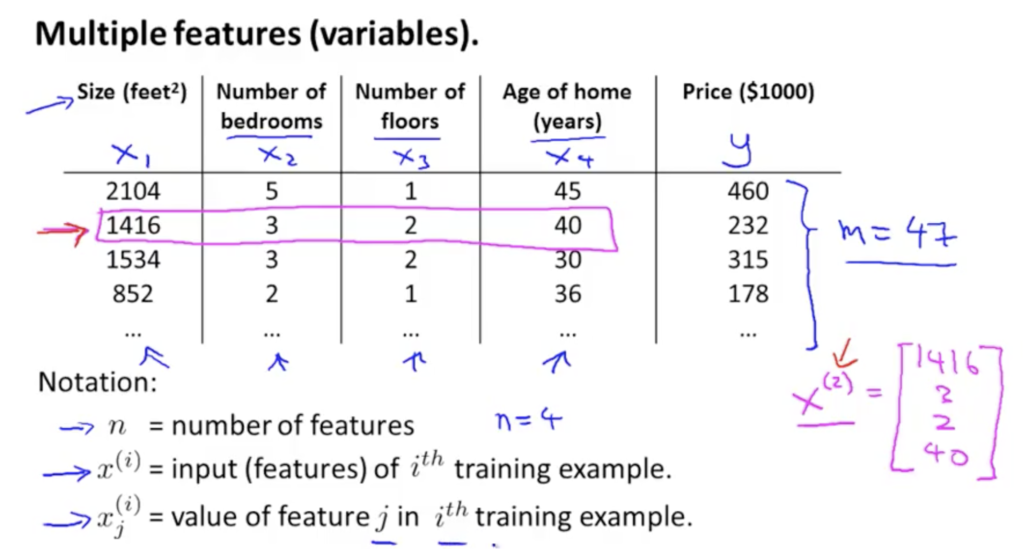
위 데이터에서 n = 4, m = 47가 된다.

x^{(2)} = \left[\begin{matrix}1416\\3\\2\\40\\\end{matrix}\right]

(2)는 x의 승수가 아니라, 2번째 값을 의미.

Hypothesis:
h_\theta(x) = \theta_0 + \theta_1x (x)
h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 + \theta_4x_4 (o)
ex) h_\theta(x) = 80 + 0.1x_1 + 0.01x_2 + 3x_3 - 2x_4

Hypothesis 함수에 대한 multivariable form은 아래를 만족한다.

h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n
For convenience of notation, define x_0 = 1 (x_0^{(i)} = 1)

위 데이터와 비교하면, 여기서 \theta_0은 basic price of a house를, \theta_1은 price per square meter를, \theta_2는 price per floor를 의미한다. x_1은 하우스당 quare meters 의 개수가 되고, x_2는 총 floor수가 된다.

x = \left[\begin{matrix}x_0\\x_1\\x_2\\...\\x_n\\\end{matrix}\right]

\theta = \left[\begin{matrix}\theta_0\\\theta_1\\\theta_2\\...\\\theta_n\\\end{matrix}\right] \in \mathbb{R}^{n+1}

\left[\begin{matrix}\theta_0&\theta_1&...&\theta_n\end{matrix}\right] \left[\begin{matrix}x_0\\x_1\\...\\x_n\end{matrix}\right]
여기서 \left[\begin{matrix}\theta_0&\theta_1&...&\theta_n\end{matrix}\right] = \theta^{T} ((n+1) x 1 행렬)이므로, \left[\begin{matrix}x_0\\x_1\\...\\x_n\end{matrix}\right]를 x로 두면

h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n
= \theta^{T}x

=> 이를 Multivariate linear regression이라고 한다.

다변수를 위한 경사하강법

Hypothesis: h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n
Parameters: \theta_0, \theta_1, .... , \theta_n => \theta
Cost Function: J(\theta_0, \theta_1, .... , \theta_n (J(\theta)) = \frac{1}{2m}\sum_{i=1}^{m}\left(h_\theta\left(x^{(i)}\right) - y^{(i)}\right)^2
Gradient descent:
Repeat {
\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J\left(\theta_0,...,\theta_n\right)
} (simultaneously update for every j = 0,….,n)

새로운 알고리즘을 적용하면 (기존에 \theta_0 \theta_1에 적용한 알고리즘을 좀더 다변수로 하여 시그마를 취함):

연습1 – Feature Scaling

Idea: Make sure features are on a similar scale.

E.g. x_1 = size(0-200 feet^2)
x_2 = number of bedroom(1-5)

단순 cost function으로는 시간이 오래걸림.

x_1 = \frac{size\left(\text{feet}^2\right)}{2000} , x_2 = \frac{\text{number of bedrooms}}{5} => 0 \leq x_1 \leq 1 0 \leq x_2 \leq 1 로 스케일링 시킴.

Mean normalization
x_i를 x_i - \mu_i로 치환시켜서 평균이 대략 0이 되게 만듬 (x_0 = 1을 사용하는게 아님)

e.g. x_1 = \frac{\text{size}-1000}{2000} ,x_2 = \frac{\text{\#bedrooms} - 2}{5} => -0.5 \leq x_1 \leq 0.5 -0.5 \leq x_2 \leq 0.5
x_1 <- \frac{x_1 - \mu}{S_1} x_2 <- \frac{x_2 - \mu}{S_2}
(여기서 \mu는 트레이닝 셋의 x의 평균)
(S_1은 (max-min)의 범위의 표준 편차)

연습2 – Learning Rate

\theta_j := \theta_j - \alpha\frac{\partial}{\partial\theta_j}J\left(\theta\right)

  • “Debugging”: 경사하강법이 정상 동작하는지 확인하는 방법
  • 어떻게 learning rate인 \theta를 정할 것인가.

정상 작동: J\left(\theta\right) 는 모든 반복에서 감소해야 한다. 하지만 어느 시점에서는 거의 변하지 않음. cost함수가 줄어들었기 떄문.
(경사 하강의 반복 숫자가 수렴하는 반복 횟수는 모든 경우에 따라 다름)
수렴하는지 확인하려면 그래프를 그려 수렴하는지 확인해야 한다. 혹은, 자동으로 수렴하는 것을 아는 방법이 있다.

자동 수렴 확인: J\left(\theta\right)의 감소량이 한번만 반복에서 10^{-3} (즉, \epsilon , 0.001) 보다 작을 때. 하지만 이 임계점을 일일히 알기는 어렵다. (그래프를 그리는 것을 추천.)

이런 그래프는 경사하강이 제대로 동작하지 않아 생김

이 경우에도 올바른 값을 못가져오므로 알파 값을 줄이면 됨.

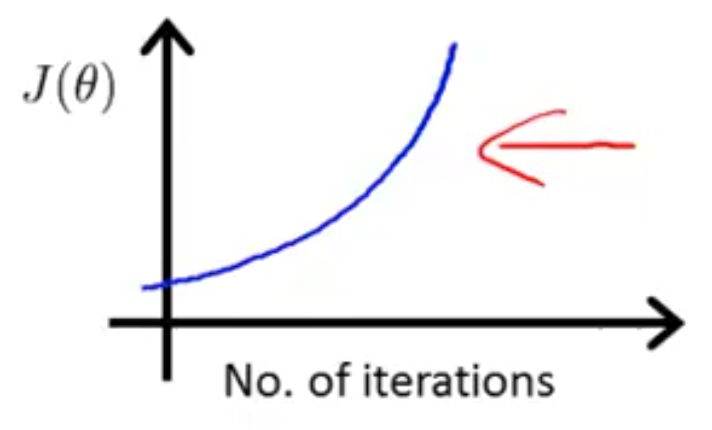
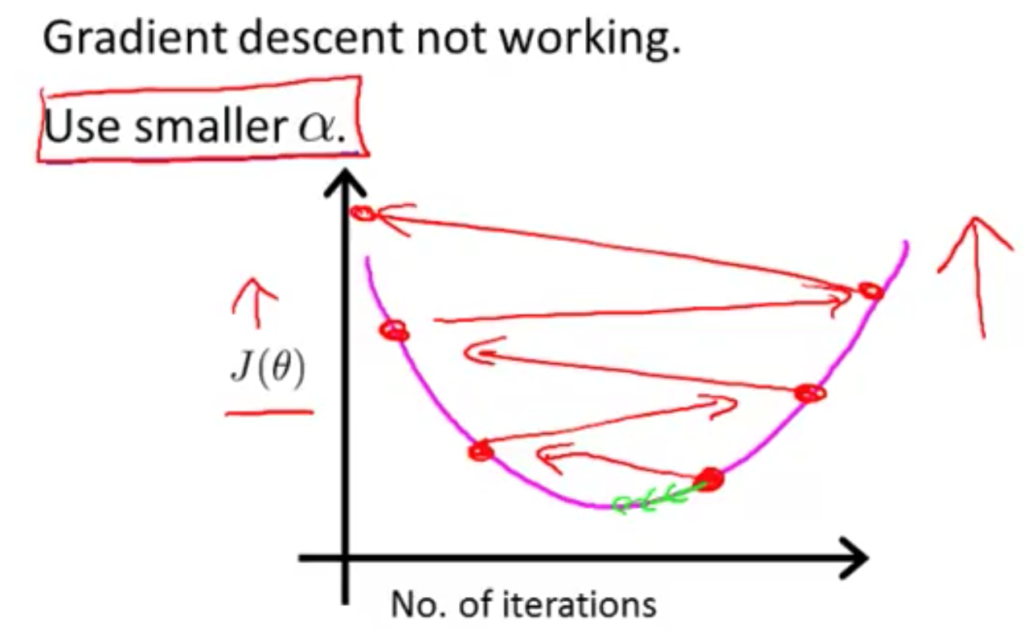
충분한 알파값을 가질 때, cost함수는 모든 반복에서 무조건 감소한다. 하지만 알파가 너무 작으면 너무 느리다. 수차례 반복하고 나서야 최소값에 도달한다.

보통 gradient descent는 0.001, 0.001, 0.1, 1 처럼 빠르게 감소할 때의 알파값을 찾은 후, 여기서 찾는다.

Features and Polynomial Regression

집값 예측 모델:
h_\theta\left(x\right) = \theta_0 + \theta_1 \times \text{frontage} + \theta_2 \times \text{depth}
여기서 frontage가 x1, depth가 x2
area => x = frontage * depth
이는 집의 넓이기 떄문에 아래와 같이 하나만 가지고 정의가 가능하다. (곱이기 떄문에)
즉, x1, x2의 두 개를 가져갈 필요는 없고, 새로운 x를 정의하면 됨.
h_\theta\left(x\right) = \theta_0 + \theta_1x

위 데이터에서 직선은 데이터를 표현하기 힘드므로, 2차함수를 사용. 하지만 2차함수는 결국 하강하므로 (집값이 하강할 일은 없으니) 3차함수를 사용하면 위 초록색 그래프처럼 결국 상승하게 되있음.

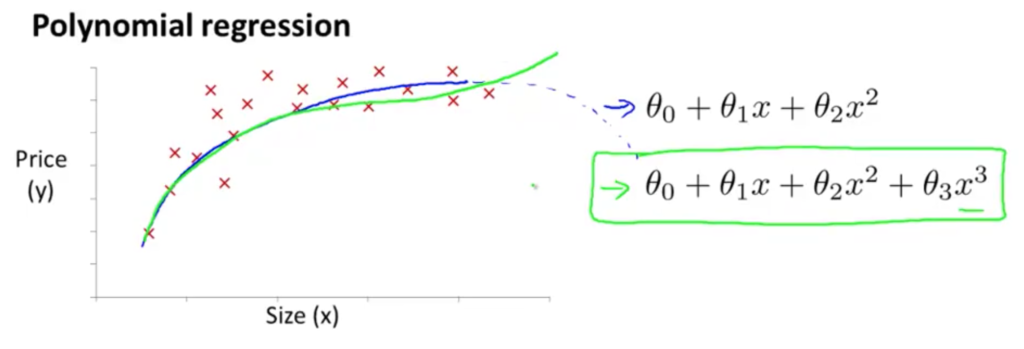
어떻게 데이터를 잘 표현하는 식을 구하나
다변수 선형 회기를 사용!

위와 같이 가설함수의 x값을 제곱/세제곱으로 치환하여 사용.

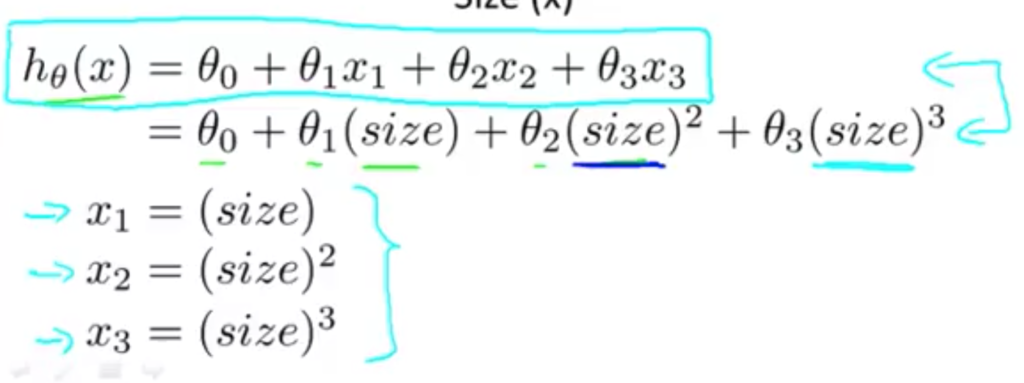
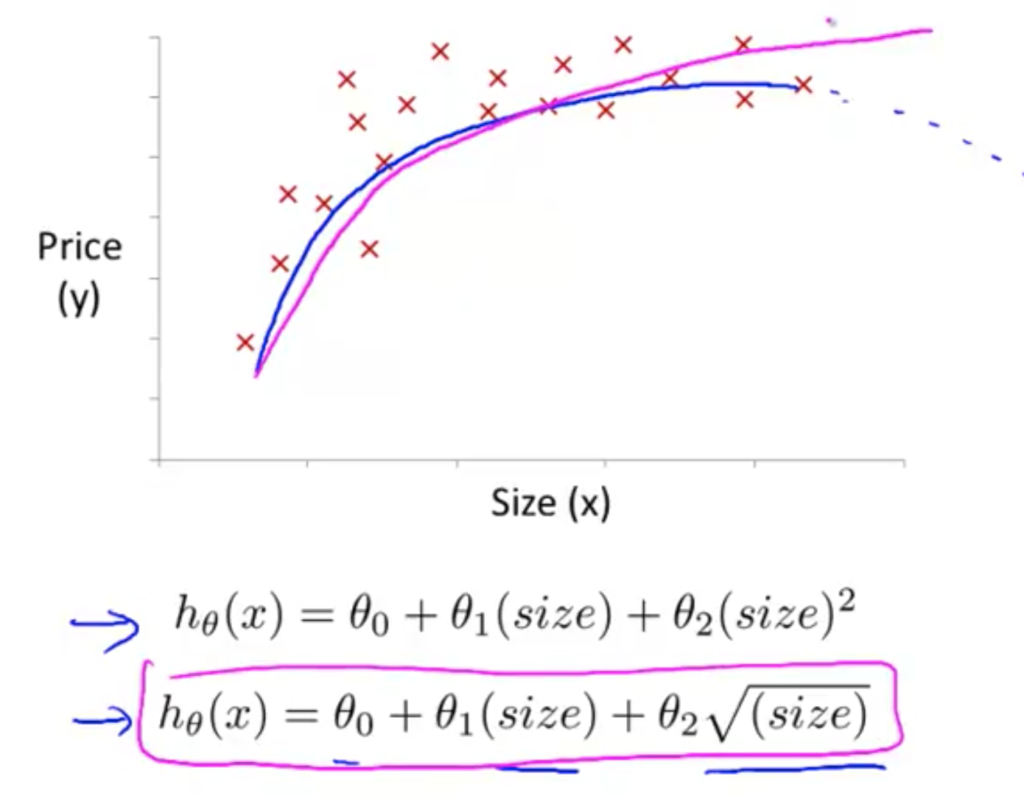
Feature의 선택

3차함수 이외에도 위에서처럼 루트함수도 올라가는 그래프가 (핑크색) 나오므로 3차함수를 대처할 수 있음.

Normal Equation

J\left(\theta\right)에서 세타 값을 “분석적(analytically)”으로 구하는 방법.

시작: 만약 1D (\theta \in \mathbb{R}) ,
J\left(\theta\right) = \alpha\theta^2 + b\theta + c

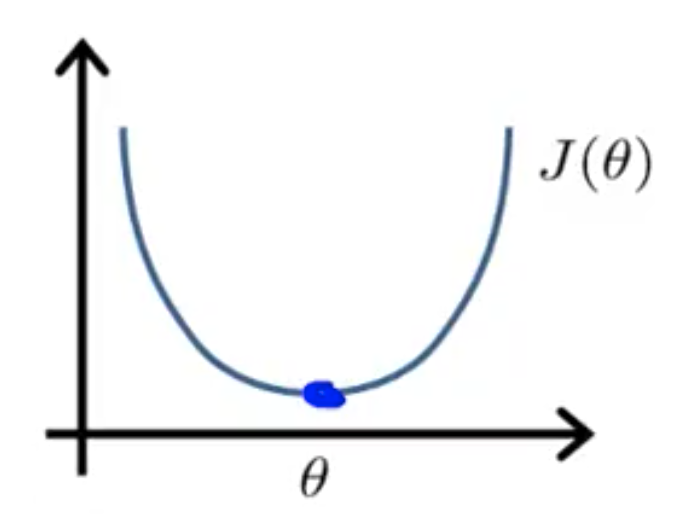
여기서 알파값을 구하는 것은 미분해서 0이되는 구간을 구하면 되긴함.
우리가 궁금해 하는 것은,
(\theta \in \mathbb{R}^{n+1} 일때
J\left(\theta_0,\theta_1,....,\theta_m\right) = \frac{1}{2m}\sum_{i=1}^{m}\left(h_\theta\left(x^{\left(i\right)}\right) - y^{\left(i\right)}\right)^2

경사하강법
(단점)
– 알파를 정해야 한다.
– 많은 반복이 필요하다.
(장점)
– n이 많을 때에도 잘 동작한다.

정규방정식(Normal Equation)
(장점)
– 알파를 정할 필요가 없다.
– 반복이 필요없다.
(단점)
– 계산이 많이 필요하다.: \left(X^{T}X\right)^{-1}을 계산하려면 n x n 을 계산해야 하므로 대략 O(\left(n^3\right)의 시간이 걸린다. (행렬의 차원의 3제곱.. 엄청 느림)
– n이 매우 크면 엄청 느리다. (반대로 n이 작으면 좋음. n이 100~1000정도면 괜찮음.)

=> 문제에 따라 선택하기!

불필요한 feature가 있는지 먼저 확인. 없으면 non-invertible문제가 해결된다.