수세기(count) -> 확률 -> 통계
확률 통계는 수세기만 잘되면 된다. 잘세는 방법: 빠짐없이 겹치지 않게 세면 되며, 덧셈과 곱셈만 잘하면 된다. 다만, 언제 더하고 언제 곱하는 상황을 구분해 내는 것이 어렵다. 즉, 이 강의에서는 어떤 경우에 대해 상황 구분을 하는지에 대해 오늘 공부.
상황구분
- “기준”을 잘 세워야 한다.
- 수형도: 규칙이 없을 때는 어쩔 수 없이 일일이 세야한다.
- 사전식배열: dictionary. abc/acb/bac/bca….
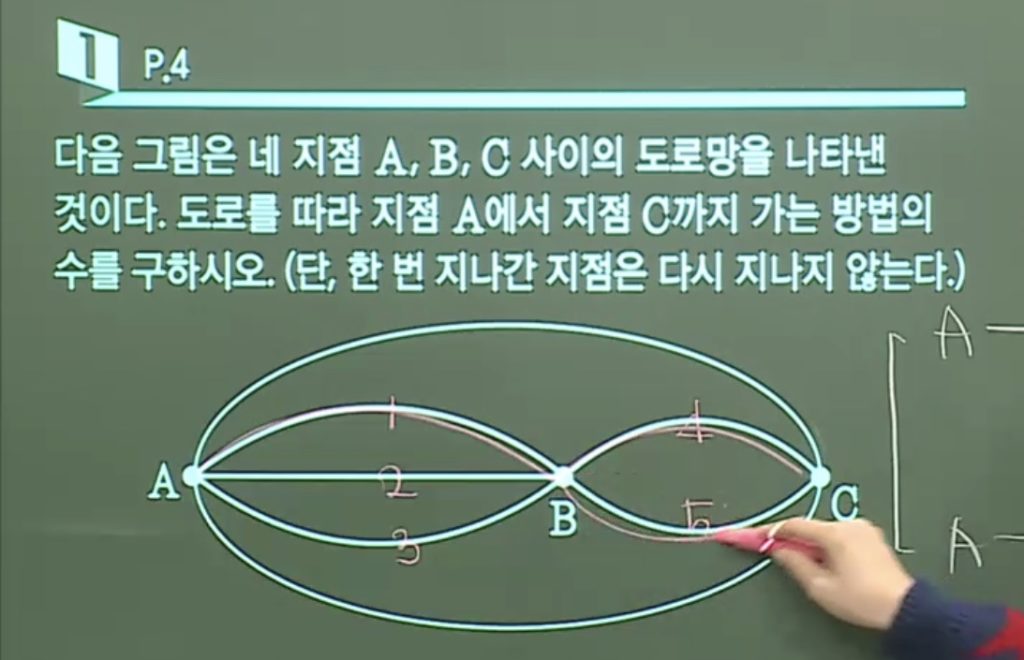
(국민예제) A->C: 1+1=2 / A -> B -> C = 3 x 2 = 6 즉 2+6 = 8가지 경우의 수.
위 문제는 언제 곱하고 더하는지 알 수 있는, 확률적 사고를 연습할 수 있는 “도로망”문제.
문제: 1,2,3,4의 번호가 적힌 4장의 카드를 일렬로 나열하는 경우의 수를 구하시오.
사전식 배열로 해볼것.
1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
2,1,3,4
….
앞자리 1의경우: 6, 2의경우: 6가지… 총 6×4가지 = 24
문제: 모자 4개를 서로 다른 네 명의 학생이 쓰고 있을 때, 서로 바꿔 쓰는 경우를 구하시오 (단, 처음에 썼던 모자는 아무도 쓰지 않는다.)
확률의 경우, 자신이 알고있는 공식?같은것이 없다면 일일이 셀 수 밖에 없다. 이 경우,사람을 A,B,C,D로 두고, 모자를 a,b,c,d로 둔 이후 수형도를 그린다.
2. 확률적 사고: 덧셈
문제: 서로 다른 두 개의 주사위를 동시에 던질 때, 나오는 수의 합이 5 또는 10이 되는 경우의 수를 구하시오.
”수작업”을 할 것.
5가되는 경우: (1,4), (2,3), (3,2), (4,1) -> 4가지
10이되는 경우: (4,6), (5,5), (6,4) -> 3가지
위 두 경우를 더한다: 4+3 = 7가지
합의법칙: 두 사건 A,B가 일어나는 경우의 수를 각각 m,n이라고 하면 두 사건 A,B가 동시에 일어나지 않을 때, A또는 B가 일어나는 경우의 수는 m+n (세개 이상의 사건도 가능하다.)
문제: 남자 5명과 여자 3명이 출연하는 방송이 있다. 이 프로그램에서 남여를 같은 수로 선택하여 게임을 시키려고 할 때, 선택할 수 있는 경우의 수를 구하는 방법을 설명하시오 (단, 한명도 선택하지 않는 경우는 없다.)
같은수의 경우: (남,여) = (1,1) (2,2) (3,3) 4명은 안됨 (여자가 최대 3명이므로)
이후 각각의 경우의 수를 구한 후, 더하면 된다. (겹치지 않으므로)
문제: 어느 행사장에서는 현수막을 1개씩 설치할 수 있는 장소가 5곳이 있다. 현수막은 A,B,C세 종류가 있고, A는 1개, B는 4개, C는 2개가 있다. 다음 조건을 만족시키도록 현수막 5개를 택하여 5곳에 설치할 때, 그 결과로 나타낼 수 있는 경우의 수를 구하는 방법을 설명하시오. (단, 같은 종류의 현수막끼리는 구분하지 않는다.)
(가) A는 반드시 설치한다.
(나) B는 2곳 이상 설치한다.
기준을 B의 갯수로 먼저 나눠서, 이를 순열(나중에 배움)로 구한 후, 이 경우를 모두 더한다.
A BBCC
A BBBC
A BBBB
3. 확률적 사고: 곱셈
예제: 햄버거, 사이드, 음료에서 각1종류씩 선택해 햄버거 세트를 주문한다고 할 때, 아래 메뉴판에서 햄버거 세트를 주문하는 방법의 수를 구하시오(단, 선택을 안하는 경우는 생각하지 않는다.)
(1) 햄버거 세트를 경우하는 방법의 수
햄버거: 불고기버거/치즈버거/새우버거거거 -> 3가지
사이드: 감튀, 치킨너겟 -> 2가지
음료: 콜라, 커피, 오랜지주스, 우유 -> 4가지
3x2x4 = 24가지. 각각에 대하여 반복적으로 일어나고 있음.
(2) 새우버거를 선택한 경우 사이드 메뉴로는 감자튀김만 주문 가능한 경우
먼저 불고기, 치즈버거 선택했을 경우: 2x2x4 = 16
새우버거의 경우: 1x1x4.= 4
이들의 합: 16 + 4 = 20
곱의 법칙:사건 A가 일어나는 경우의 수가 m이고, 그 각각에 대하여 사건 B가 일어나는 경우의 수가 n일때, 두 사건 A,B가 동시에(함께,연이어,잇달아) 일어나는 경우의 수는 mxn (세개 이상의 사건에도 성립한다.)