2019년 10월 12일

최은진의 노베부터 시작하는 확통 20 – 03강 여러 가지 순열(1)

원순열

서로 다른 n개를 원탁에 나열. \frac{n!}{n} => n으로 나눔 (돌렸을 때 같은 것의 개수, 돌.같.개 ….)

원탁에 배열후 돌렸을 때도 같은 경우는 같은 경우로 취급.
예: ABC를 배열
ABC ACB
BAC BCA
CAB CBA
=> ABC, BCA, CAB는 같음.
=> ACB, BAC, CBA 는 같음.
=> 답은 2가지.

문제: A,B,C,D를 원탁에 배열하는 경우의 수를 구하시오 (단, 회전해서 같은 것은 같은 경우로 본다.)

(1) <나열 후 취소>의 관점: \frac{4!}{4} = 3! = 6
(2) <한명을 고정>시키는 관점: 그냥 3! = 6

문제: 그림과 같은 정사각형 모양의 탁자에 8명의 사람이 앉는 경우의 수를 구하시오(단, 회전해서 같은 것은 같은 경우로 본다.)

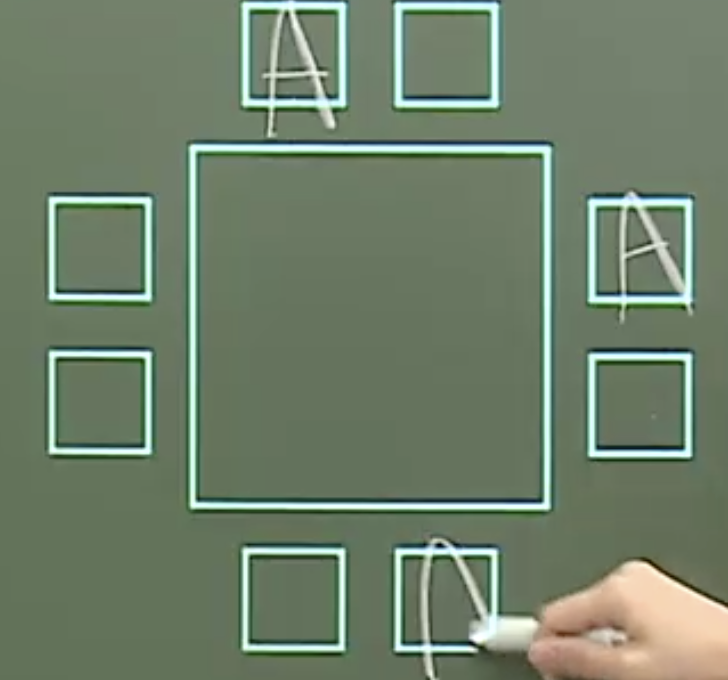
(1) <나열 후 취소>의 관점: \frac{8!}{4} => 모서리에 왔을때만 같다!
(2) 원순열을 이용: 정사각형을 원이라고 생각. 두 가지의 경우가 다르기 때문에, 7! x 2 즉 2가지는 다른 경우이므로(돌렸을 때 다른 것의 갯수)

문제: 그림과 같은 직사각형 모양의 탁자에 10명의 사람이 앉는 경우의 수를 구하시오(단, 회전해서 같은 것은 같은 경우로 본다.)

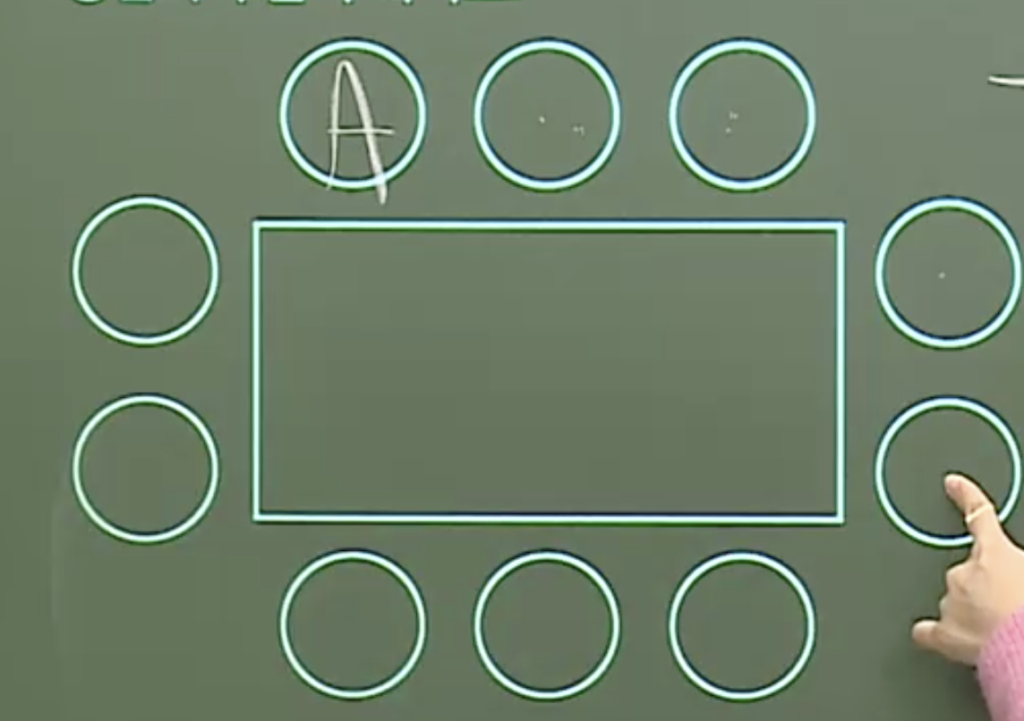
10!에 전체적으로 봤을 때, 아래쪽 처음에 앉았을 경우에만 같으므로, 2가지의 돌렸을 때 같은 것의 개수가 나옴. 즉, 10! / 2

Or, 원순열을 이용. 9! x 5 (5가지의 다른 개수)

같은것이 있는 순열

a,a,b일렬로 나열
-> a1, a2, b
a1, a2, b a2, a1, b b, a1, a2
a1, b, a2 a2, b, a1 b, a2, a1
=> 여기서 a1, a2, b = a2, a1, b / a1, b, a2 = a2, b, a1 / b, a1, a2 = b, a2, a1
즉, 나열했을 때 같은 것의 개수(묶음의 개수)로 나누면 됨. 즉, \frac{3!}{2} 즉 같은 것의 개수.

문제: 5개의 문자 a,a,a,b,b를 일렬로 배열하는 경우의 수를 구하시오.

5!에 3!x2!로 나눠줌. 즉, a의 배열의 경우의 수와 b의 경우의 수. 답 10개

문제: 1부터 6가지의 자연수가 하나씩 적혀 있는 6장의 카드가 있다. 이 카드를 모두 한 번씩 사용하여 일렬로 나열할 때, 2가 적혀 있는 카드는 4가 적혀있는 카드보다 왼쪽에 나열하고 홀수가 적혀있는 카드는 작은 수부터 크기 순서대로 왼쪽에 나열하는 경우의 수를 구하시오.

1 3 5는 무조건 1,3,5의 순서로 => 한문자로 생각하고 나열. => 1로 가정
2와 4도 한문자로 생각하고 나열 => 2로 가정
1,2,1,2,1,6 즉, \frac{6!}{3!2!}
순서가 정해져 있다 = 같은것이 있는 순열이다.

문제: 6개의 문자 a,a,a,b,b,c중에서 4가지를 선택하여 일렬로 나열할 때, 만들 수 있는 서로 다른 문자열의 개수를 구하시오.

-> 공식이 없음! 수작업으로 케이스를 나눌 것.

  • a를 1개 쓰는경우
    • a b b c => 4! / 2!
  • a를 2개 쓰는경우
    • a a b b => 4! / (2!2!)
    • a a b c => 4! / 2!
  • a를 3개 쓰는경우
    • a a a b = > 4! / 3!
    • a a a c => 4! / 3!

모든 케이스를 더함. 즉, \frac{4!}{2!}\ast2 + \frac{4!}{2!2!} + \frac{4!}{3!}\ast2 = 38

최단거리 길 찾기

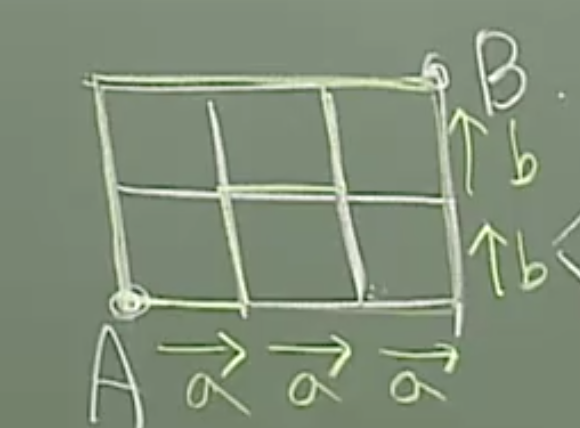
같은 순열의 법칙을 위처럼 a와 b로 두고 aaabb 의 배열로 응용. 즉, \frac{5!}{3!2!}
혹은 센다의 법칙 => 각 지점에 갈 수 있는 경우를 모두 합침

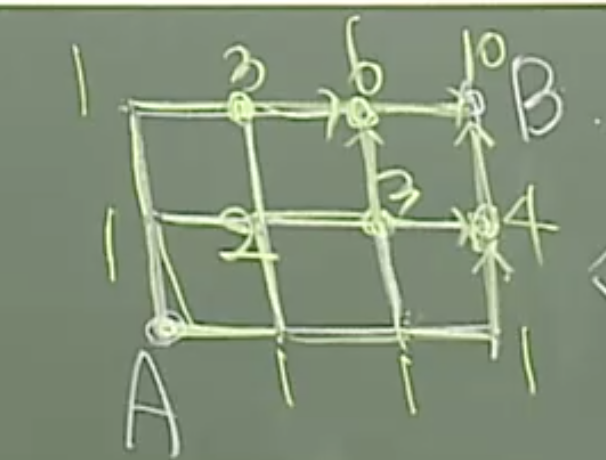
문제:

A -> P로 가는 경우 2가지
P->Q로 가는 경우 2가지
Q->B로 가는 경우는 \frac{4!}{2!2!}가지
즉 모두 곱해줌.

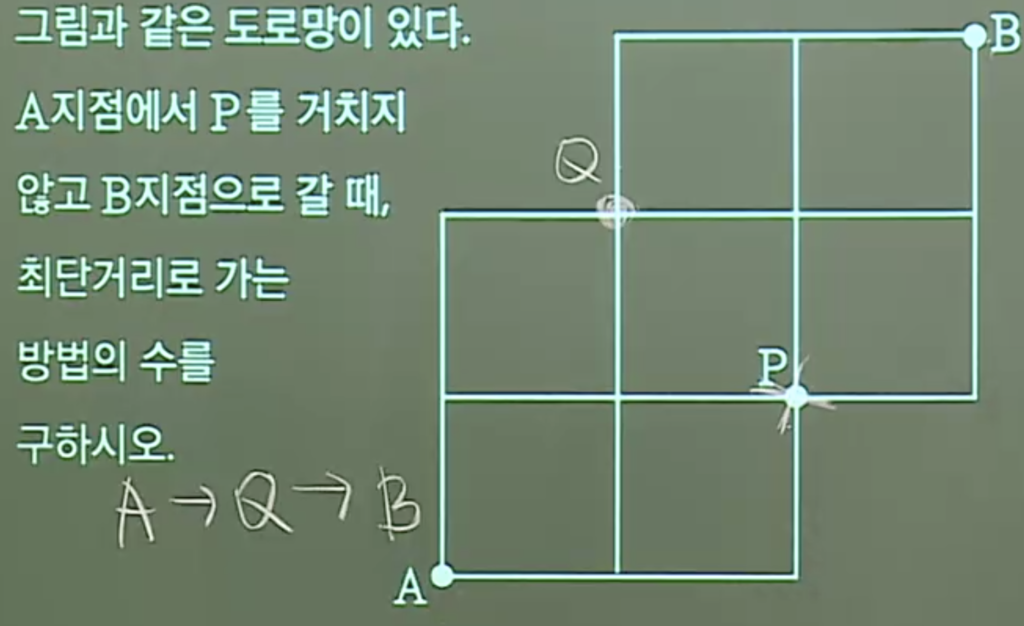
A -> Q -> B로 가는 경우밖에 없음.
(3! / 2! ) * (3! / 2!) = 9

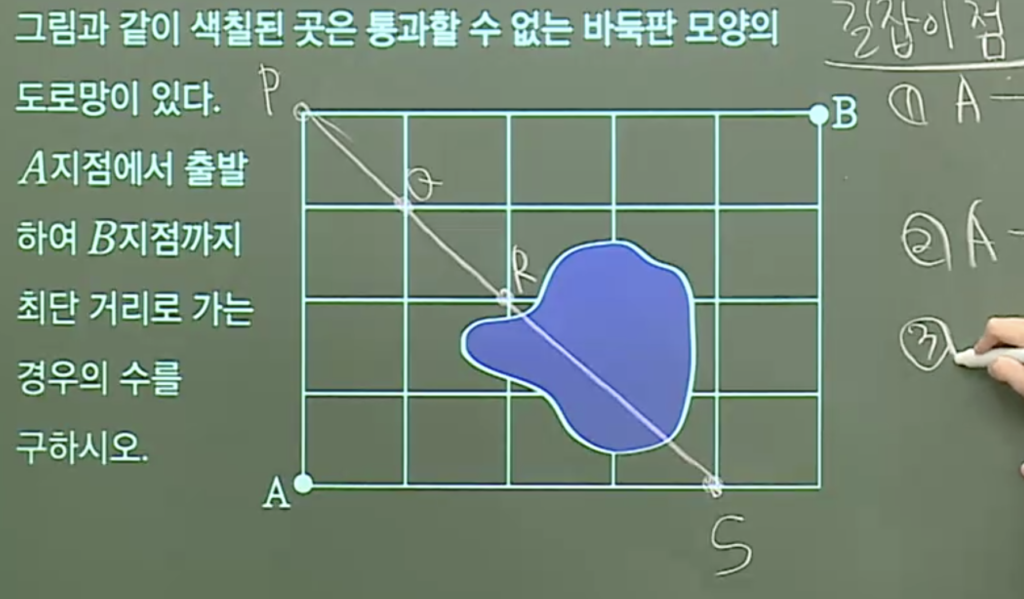
“길잡이점” 을 통해 위 그림처럼 PQRS를 (꼭 지나갈 수 밖에 없는) 정점을 찾는다.
(1) A -> P -> B => 1가지
(2) A -> Q -> B -> 4!/3! * 5!/4! = 20
(3) A -> R -> B -> 3!/2! * 1 * 1 * 4!/3! = 12
(4) A -> S -> B -> 1 * 5!/4! = 5
즉, 38가지.